So far we have derived the equation for wave profile at time t by moving the coordinate frame of the wave in time. This results in the expression for the profile of a plane progressive wave. However, we can also move the coordinate frame at certain time by introducing the so-called wavephase 
. This quantity is particularly useful when we have more than one wave, and we need to determine their relative locations at certain time.
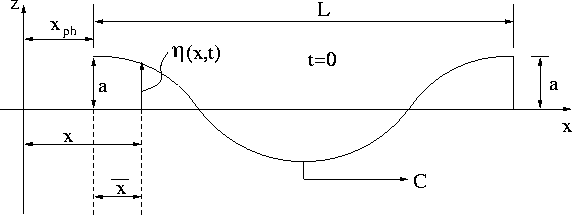
Figure 5: Progressive Wave with Phase
A more general expression for the waveform of a plane progressive plane is given by:
Let us examine the above equation at time t = 0. From Figure 5 the waveform is shifted by
Therefore, the expression for the waveform at t = 0 can be written as:
Notice that minus sign in front of indicates the wave is shifted in the positive X direction.
