The simplest mathematical function for describing waves is the sine (or cosine) function. Waves that can be modeled by a single function are called simple waves. More complex waves can then be represented by superposition or expansion of simple waves. Sine function can be conveniently used to describe a simple wave due to its harmonic or periodic property, which is consistently preserved by any linear mathematical operations (addition, differentiation, integration, etc.).
In water-wave theory, sinusoidal waves are often called small-amplitude or linear waves. Since they are periodic in both space and time, they are also called regular waves. A more detailed description on various wave theories and their derivations will be given in the subsequent chapters.
We will start with some basic terms necessary to define the characteristic of a sinusoidal wave as shown in Figure 1. These terms were cited from [1].
=wave elevation (local, function of x)
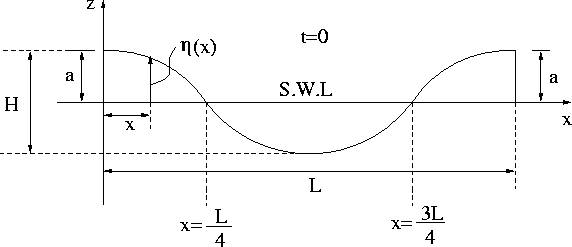
Figure 1: Wave Profile at Time t=0
Two parameters are needed to describe a sinusoidal wave, such as the period (T) and the height (H). The other properties, e.g. wavelength, speed, and frequency, can be properly derived from them. The general expression for a plane progressive wave is given by:
where a is the wave amplitude 
, k and 
are constants to be determined. We will see that these two constants have physical meaning.
Let us now consider a wave profile at time t = 0 as shown in Figure 1. Inserting t = 0 into equation 1 gives the wave profile as:
To determine k, we insert the condition at x = L into equation 2 as follows:
The constant k is called the wave number. Therefore, equation 2 can be written as:
The plane progressive wave moves or propagates at the speed or celerity C. Let us consider the wave profile at time t as shown in Figure 2. Since at time t the wave profile is exactly the same as that at time t = 0, we simply moves the origin of the wave at a distance of 
, where:
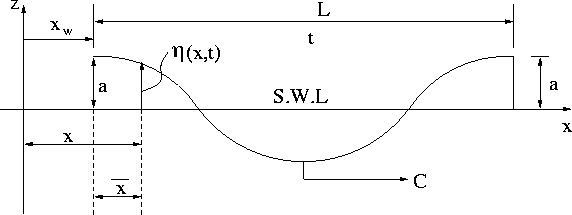
Figure 2: Wave Profile at Time t
Denoting the new coordinate frame of the wave by 
, we can write the equation for the wave profile as:
where
Using relationship 5, we obtain:
Refering to the definition of wave period, wavelength and celerity, we can write the relationship between these quantities as:
Substituting the above relationship to equation 8 results in the expression for the profile of a plane progressive wave:
The constant 
is called the angular frequency of the wave in radians/second. The relationship between the angular frequency and the frequency can be written as:
Equation 10 is valid for the waves traveling in the positive x direction. The wave profile of a plane progressive wave traveling in the opposite direction can be derived by reversing the sign of the wave celerity C in equation 8 (See Figure 3). This results in:
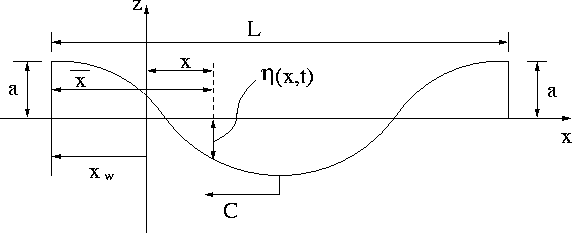
Figure 3: Progressive Wave Traveling in -X direction
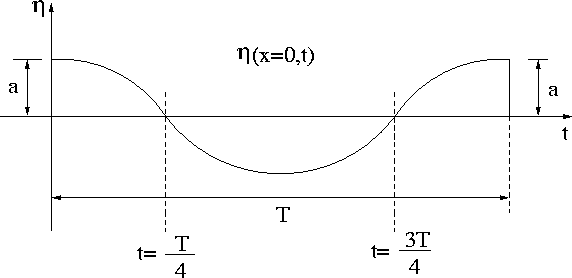
Figure 4: Time History at Location x=0
Equation 10 can also be used to determine the time history of a certain point as the wave passes through it. Let us examine the time history at point x = 0 as the wave propagates in time. Inserting x = 0 into equation 10 leads to:
which clearly shows that the sinusoidal wave is also periodic in time (see Figure 4)
