It can be shown that the velocity potential can be put in the form:
with 
and A being constants to be determined.
must satisfy Laplace equation
is excluded because 
would grow exponentially with 
, 
corresponds to a non-physical solution.
must satisfy the kinematic b.c. on the free surface:
Deep Water
Dynamic b.c. must also be satisfied on the free surface: ( 
)
So eqn.(14) becomes:
is second order (linear wave theory)
Eqn. (23) is called the dispersion relationship (Deep Water)
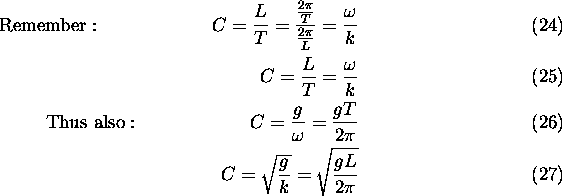
Deep Water
so as L 
or T 
C
From the three quantities C,L,T, only one can be given. The other two can be expressed in terms of the given quantity.
