CE319F (© Kinnas) FALL 1998
Derivation of Bernoulli's equation along a streamline

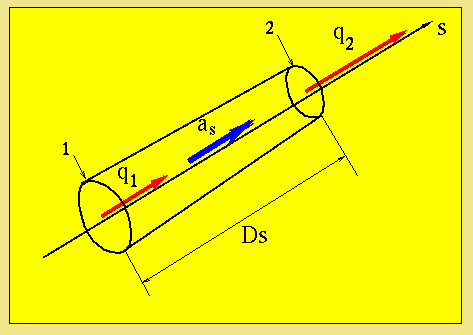
Euler's equation applied along the streamline s:

Dt can be related with Ds via the mean velocity between points 1 and 2.

Replacing Dt from equ. (3) into equ. (2) we get:

as Ds goes to zero the above equation becomes:

Replacing the above expression for the acceleration into the Euler equation (1) and re-arranging we get (we also assume that the fluid is incompressible at this point):

The above equation renders Bernoulli's equation along a streamline:

or in the form (after dividing by gamma=rho.g):

Definitions:

• First two terms in the above equation : piezo-metric head
• q^2/(2g) : velocity head
• H: total head

Assumptions in Bernoulli's equation. The flow must be:

• inviscid
• incompressible
• steady

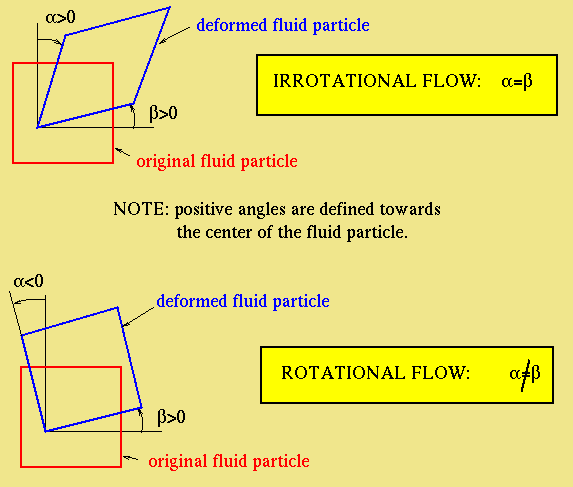
In order for Bernoulli's equation to be valid everywhere in the flow-field (and not only along a streamline), the flow also must be irrotational. The proof will NOT be covered in CE319F. For those who are interested a proof may be found in the classnotes of CE358 (Introductory Ocean Engineering) by S.A. Kinnas, where also the generalization of Bernoulli's equation in the case of unsteady flows is given.

Examples of rotational and irrotational flows are shown in the next figures. The flow close to fixed boundaries (where the effects of viscosity are also predominant) or downstream of bodies is considered rotational. However, the flow away from the above regions can be considered as irrotational.